Die Boolesche Algebra ist die mathematische Grundlage für logische Verknüpfungen. Sie ist auf den Mathematiker George Boole (1815 - 1864) zurück zuführen, der im 19. Jahrhundert die Algebra der binären logischen Verknüpfungen entwickelte.
Die Boolesche Algebra umfasst die Mengenalgebra, Schaltalgebra, Aussagenlogik und die Wahrscheinlichkeitsrechnung und bildet die Berechnungsgrundlage für die Dualarithmetik und somit für die hard- und softwaretechnischen Computerfunktionen. Sie basiert ausschließlich auf binären Werten, wobei die Operatoren zwei Eingangswerte mit einem Ausgangswert verknüpfen.
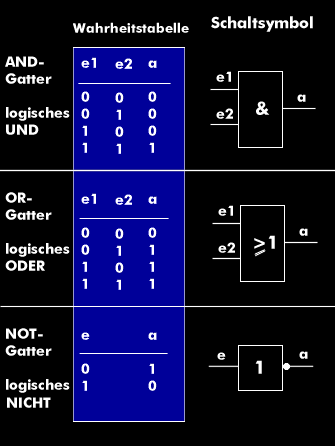
Die beiden Grundfunktionen der Schaltalgebra sind die Und- Verknüpfung (A*B) und die Oder-Verknüpfung (A+B), die man sich analog als Schaltfunktion vorstellen kann. Die Und-Funktion, das AND-Gatter, bildet eine Reihenschaltung zweier Schalter. Erst wenn beide Schalter geschlossen sind, kann Strom über die Schalter fließen. Bei der Oder-Funktion, dem OR-Gatter, kann man sich die Schalter in Parallelschaltung vorstellen. Der Strom fließt über die Schalter, sobald ein oder beide Schalter geschlossen sind. Ein weiteres Grundelement der Booleschen Operatoren ist der Nicht- Operator, das NOT-Gatter, das nur einen Operanden benutzt und die Funktion eines Inverters ausführt.
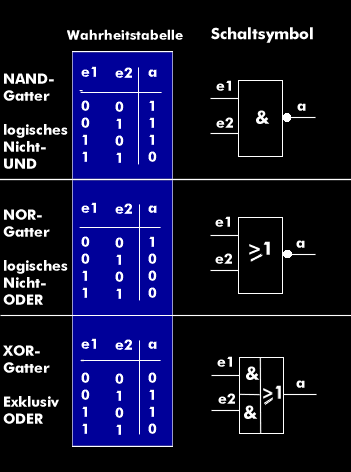
Die Und-Verknüpfung stellt die Konjunktion zwischen den Eingängen her, die Oder-Verknüpfung die Disjunktion, die NOT-Verknüpfung die Negation und die XOR-Verknüpfung die Antivalenz. Aus diesen Grundfunktionen werden alle anderen Verknüpfungen abgeleitet: NOR-Gatter, XOR-Gatter, NAND-Gatter, XNOR-Gatter, Volladdierer und Halbaddierer
Die Ergebnisdarstellung erfolgt in tabellarischer Form unter Auflistung der logischen Zustände an allen Ein- und Ausgängen. Diese Tabelle heißt Wahrheitstabelle.
Spezielle Gesetze der Booleschen Algebra
In der Booleschen Algebra gibt es mehrere Gesetze zur Vereinfachung der Rechenoprtation. So das Common Identities Law, das für den mathematischen Ausdruck A(A + B) = AB oder A + AB = A + B steht. Dieser Ausdruck kann auf AB reduziert werden ohne den Rechenvorgang fortzuführen. Ein weiteres Gesetz ist das Commutative Law. Dieses Gesetz besagt, dass die Änderung der Reihenfolge der Variablen keine Auswirkung auf das Ergebnis hat. Beispiel: A + B = B + A; A x B = B x A. Das Complementary Law besagt, dass die Addition eines Betrags und ihres Komplements immer 1 ist, und dass die logische Multiplikation eines Betrags und dessen Komplements 0 ist.