Die Dualarithmetik ist die Anwendung der Arithmetik des Addierens, Subtrahierens, Multiplizierens und Dividierens auf das Dualsystem, also alle Rechenoperationen basierend auf den Binärziffern 0 und 1. Die Dualarithmetik bildet die Basis für alle digitalen Recheneinheiten.
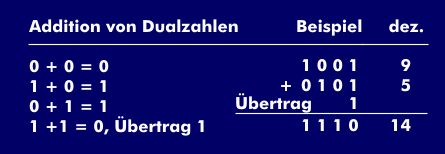
Die Addition zweier Dualzahlen ist vergleichbar der von Dezimalzahlen: "0" plus "0" ergibt "0", "1" plus "0" ergibt "1". Ausnahme bildet die Addition von "1" plus "1", das einen Übertrag von "1" hervorruft. Diese mathematische Operation führt der Volladdierer aus, bei dem der Überlaufwert auf den nächst höheren Volladdierer geführt wird.
Gleiches gilt für die Subtraktion zweier Dualzahlen: "0" minus "0" ergibt "0", "1" minus "1" ergibt "0", "1" minus "0" ergibt "1" und bei "0" minus "1" entsteht ein Übertrag von "1".
Die Multiplikation zweier Dualzahlen wird vergleichbar gehandhabt wie die Multiplikation von Dezimalzahlen.
Bei der Multiplikation werden die Eingaben mit jedem einzelnen Bit multipliziert und anschließend wird die Summe gebildet. Die Multiplikation einer vierstelligen Dualzahl mit "0" ergibt "0000", bei der Multiplikation mit "1" bleibt die ursprüngliche Dualzahl erhalten. Bei der Multiplikation mit Dualzahlen kann die Stelligkeit des Ergebnisses stark ansteigen. Wenn also zwei 4-Bit-Zahlen miteinander multipliziert werden, kann das Ergebnis eine 6-, oder 7-stellige Zahl sein.
Die Division von Dualzahlen wird auf die Subtraktion zurückgeführt. Dabei wird der Divisor so oft vom Dividenden subtrahiert, bis dieser kleiner ist als der Divisor. Der ermittelte Quotient entspricht der Anzahl der Subtraktionen. Wird beispielsweise die Zahl 60 durch 12 dividiert, dann wird die 12 von 60 subtrahiert, dann wiederum von den Zwischenergebnissen 48, 36, 24 und 12. Insgesamt konnten 5 Subtraktionen durchgeführt werden, bevor der Dividend kleiner wurde als der Divisor. Das Ergebnis ist also 5.