dual arithmetic
Dual arithmetic is the application of the arithmetic of addition, subtraction, multiplication and division to the dual system, i.e. all arithmetic operations based on the binary digits 0 and 1. Dual arithmetic forms the basis for all digital arithmetic units.
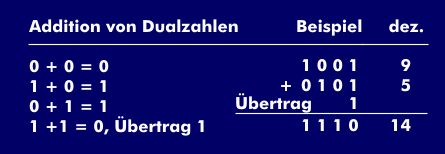
The addition of two dual numbers is comparable to that of decimal numbers: "0" plus "0" results in "0", "1" plus "0" results in "1". The exception is the addition of "1" plus "1", which produces a carry of "1". This mathematical operation is performed by the full adder, where the overflow value is carried to the next higher full adder.
The same applies to the subtraction of two dual numbers: "0" minus "0" results in "0", "1" minus "1" results in "0", "1" minus "0" results in "1" and "0" minus "1" results in a carry of "1".
The multiplication of two dual numbers is handled similarly to the multiplication of decimal numbers.
In multiplication, the inputs are multiplied by each bit and then the sum is formed. Multiplying a four- digit dual number by "0" results in "0000"; multiplying by "1" preserves the original dual number. When multiplying with dual numbers, the digitness of the result can increase greatly. So if two 4-bit numbers are multiplied together, the result can be a 6, or 7 digit number.
The division of dual numbers is traced back to subtraction. The divisor is subtracted from the dividend until it is smaller than the divisor. The determined quotient corresponds to the number of subtractions. For example, if the number 60 is divided by 12, then the 12 is subtracted from 60, then again from the intermediate results 48, 36, 24 and 12. A total of 5 subtractions could be performed before the dividend became smaller than the divisor. So the result is 5.