tree structure
One of the most important data structures in computer science is the tree structure, which is often represented in the form of a graph. It offers both the possibility to find data quickly and to store them sorted. The tree structure is excellent for describing hierarchical relationships. The applications of tree structures are manifold; for example, grammatical structures, hierarchically structured parts lists or the structure of file systems are mappings of tree structures.
Searching for an element in large amounts of data is often time-consuming - if the position is not known - if the search is performed sequentially element by element. Another possibility of finding data quickly and storing it sorted at the same time is offered by the so-called tree structure in addition to the hash table. In contrast to linear lists, trees are a branched structure; they are therefore non-linear. Thereby a tree is a recursive data structure, since it can be represented again by a set of subtrees.
For terminology related to tree structures:
Tree Set of nodes and edges
Node Represents an arbitrary object.
EdgeConnection between two nodes. It is also used to denote the branches of a tree.
Path A sequence of different nodes connected by edges.
Root A distinguished node that has no predecessors.
Leaf Node without successors.
Father Predecessor of a node.
Child Successor of a node.
Inner node Non-leaf.
Sibling Node with same father.
Height This is the name given to the highest level of a tree. The root of a tree is always at level 0.
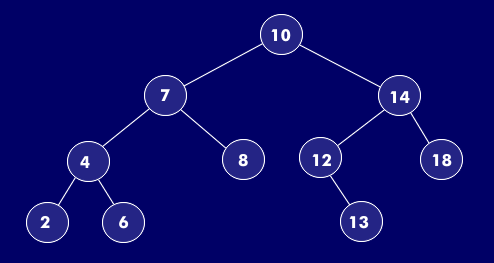
In computer science, a tree always starts "at the top" with the root. So the numbering of the nodes is from top to bottom, from left to right starting with 1. The drawing clarifies this structure and leads to the following observation:
A node i always has the successor 2i and 2i+1
From this it can be concluded that nodes can be stored in an array - respecting the indexing starting with 0 in general.
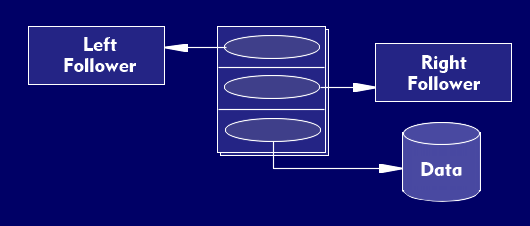
A separate form of a graph are binary trees. A binary tree occurs when each element has at most two successors (n(max) = 2). One speaks of a right and a left successor. Each element can contain three pointers: One each for the left and the right successor, and another as a reference to the data. A binary tree analogous to the figure is called complete if at least one node that is not an end node has only one successor. For example, the Unix file system is a tree, but not a binary tree, because a directory can contain more than 2 files.
To handle tree structures, the most important operations are finding a node, inserting a new node, and removing a node.
In computer science, the nodes in a tree are especially interesting when they represent objects from reality such as people, car parts, or airplane reservations. The different objects are distinguished by their so-called key value. Thekey value represents the value of an object, which is used to search for the object or to perform other operations on the object.
Tree structures are among the most important data structures in computer science and are used in various segments; for example, to organize a sorting process, to find elements in ordered sets, to organize successive decisions, or to represent the syntactic structure of sets of rules, grammars, or programs.