Eine der wichtigsten Datenstrukturen in der Informatik ist die Baumstruktur, die häufig in Form eines Graphen dargestellt wird. Sie bietet sowohl die Möglichkeit, Daten schnell aufzufinden, als auch diese sortiert zu speichern. Die Baumstruktur ist hervorragend geeignet, um hierarchische Zusammenhänge zu beschreiben. Die Anwendungen von Baumstrukturen sind vielfältig; beispielsweise sind grammatikalische Gebilde, hierarchisch aufgebaute Teilelisten oder die Struktur von Dateisystemen Abbildungen von Baumstrukturen.
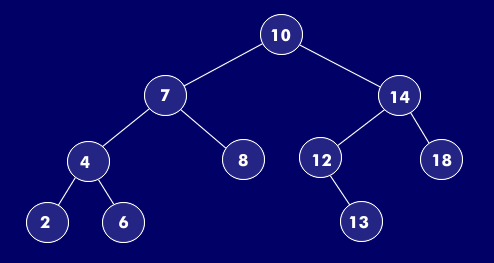
Die Suche nach einem Element in großen Datenmengen ist - sofern die Position nicht bekannt ist - oft zeitaufwändig, sofern die Suche sequentiell Element für Element durchgeführt wird. Eine andere Möglichkeit, Daten schnell aufzufinden und diese dabei auch noch sortiert zu speichern, bietet neben der Hashtabelle die sogenannte Baumstruktur. Bäume sind im Gegensatz zu den linearen Listen eine verzweigte Struktur; sie sind also nichtlinear. Dabei ist ein Baum eine rekursive Datenstruktur, da er sich wiederum durch eine Menge von Teilbäumen darstellen lässt.
Zur Terminologie im Zusammenhang mit Baumstrukturen:
Baum Menge von Knoten und Kanten
Knoten Repräsentiert ein beliebiges Objekt.
Kante Verbindung zwischen zwei Knoten. Damit bezeichnet man auch die Äste eines Baumes.
Pfad Folge unterschiedlicher, durch Kanten verbundener Knoten.
Wurzel Ausgezeichneter Knoten, der keine Vorgänger hat.
Blatt Knoten ohne Nachfolger.
Vater Vorgänger eines Knoten.
Kind Nachfolger eines Knoten.
Innerer Knoten Nicht-Blatt.
Geschwister Knoten mit gleichem Vater.
Höhe So nennt man die größte Stufe eines Baumes. Die Wurzel eines Baumes liegt immer auf Stufe 0.
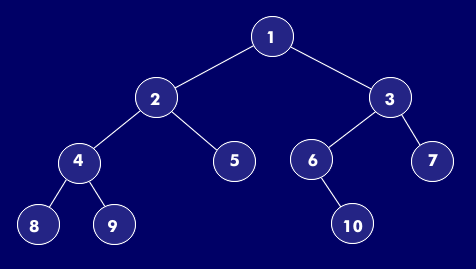
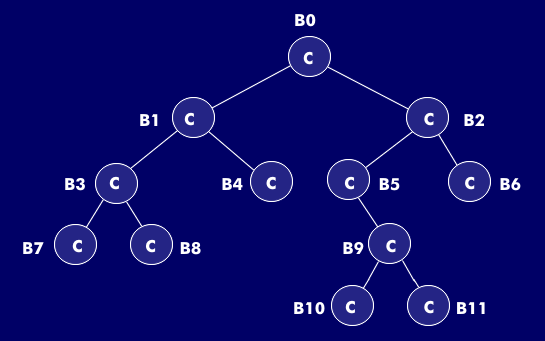
Dabei beginnt in der Informatik ein Baum immer "oben" mit der Wurzel. Die Nummerierung der Knoten erfolgt also von oben nach unten, von links nach rechts beginnend mit 1. Die Zeichnung verdeutlicht diesen Aufbau und führt zu folgender Beobachtung:
Ein Knoten i hat immer den Nachfolger 2i und 2i+1
Daraus lässt sich der Schluss ziehen, dass Knoten in einem Array abgelegt werden können - unter Beachtung der im Allgemeinen mit 0 beginnenden Indizierung.
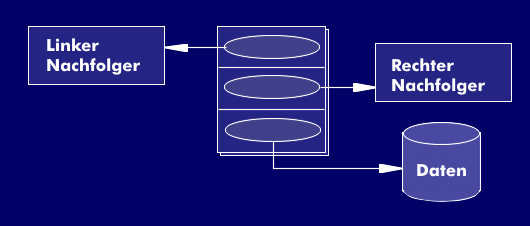
Eine gesonderte Form eines Graphen sind Binärbäume. Ein Binärbaum entsteht dann, wenn jedes Element höchstens zwei Nachfolger hat (n(max) = 2). Man spricht von einem rechten und einem linken Nachfolger. Jedes Element kann drei Zeiger enthalten: Je einen für den linken und den rechten Nachfolger, einen weiteren als Verweis auf die Daten. Ein Binärbaum analog der Abbildung heißt vollständig, wenn mindestens ein Knoten, der nicht Endknoten ist, nur einen Nachfolger besitzt. Das Unix- Dateisystem ist beispielsweise ein Baum, aber kein Binärbaum, da ein Verzeichnis mehr als 2 Dateien enthalten kann.
Zur Behandlung von Baumstrukturen sind die wichtigsten Operationen das Suchen eines Knotens, das Einfügen eines neuen Knotens und das Entfernen eines Knotens.
In der Informatik sind die Knoten in einem Baum vor allem dann interessant, wenn sie Objekte aus der Wirklichkeit so wie Menschen, Autoteile oder Flugzeugreservierungen darstellen. Die verschiedenen Objekte werden durch ihren sogenannten Schlüsselwert unterschieden. Der Schlüsselwert ( key) bildet den Wert eines Objektes ab, der benutzt wird, um nach dem Objekt zu suchen oder andere Operationen auf dem Objekt auszuführen.
Baumstrukturen gehören zu den wichtigsten Datenstrukturen der Informatik und finden Anwendung in unterschiedlichen Segmenten; beispielsweise zur Organisation eines Sortierprozesses, zum Auffinden von Elementen in geordneten Mengen, zur Organisation sukzessiver Entscheidungen oder zur Repräsentation der syntaktischen Struktur von Regelwerken, Grammatiken oder Programmen.