Die Backus-Naur-Form ist ursprünglich ein Beschreibungsmittel für die formalen Regeln - das bedeutet die Syntax - einer höheren Programmiersprache, und wird auch als Metasprache bezeichnet. Damit ist die Backus-Naur-Form eine textbasierte Alternative zu Syntaxgraphen. Angewendet wird sie jedoch auch auf die Notation von allgemeinen Befehlssätzen u.a. für Kommunikationsprotokolle. Mit der Backus-Naur-Form ergibt sich die Möglichkeit zur Darstellung von kontextfreien Grammatiken, die wiederum den Typ-2-Grammatiken in der Chomsky-Hierarchie zuzuordnen sind. Die Backus-Naur-Form wurde nach ihren Urhebern - den Informatikern John Backus und Peter Naur - benannt, die diese Darstellungsform erstmals zur Definition der Sprache ALGOL 60 angewendet hatten.
Zur Darstellung in der Backus-Naur-Form werden anstelle des Gleichheitszeichens bzw. des Vereinigungsoperators die metalinguistischen Konnektoren:
::= als Definitionszeichen und
l als Oderzeichen verwendet.
Auf die explizite Darstellung des Verkettungsoperators wird verzichtet. Jede Backus-Naur-Regel definiert eine syntaktische Kategorie, die durch eine metalinguistische Variable bezeichnet wird. Prinzipiell besteht eine Regel aus drei Bestandteilen:
- die durch eine metalinguistische Variable bezeichnete Kategorie links vom Definitionszeichen,
- das metalinguistische Definitionszeichen ::=
- die rechts vom Definitionszeichen stehende syntaktische Formel.
- Bedeutung der bezeichneten syntaktische Kategorie (z.B. ganzzahlige Konstante, Marke),
- Syntaktische Struktur (z.B. Liste, Vereinbarungsteil) und
- die Verwendung (z.B. obere Grenze, Laufvariable) hinweist.
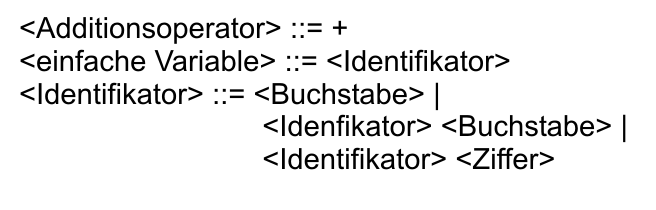
Die Backus-Naur-Regel zur Definition eines Identifikators ist hier offensichtlich rekursiv. Die Rekursionstiefe ist in dieser Backus-Naur-Regel nicht begrenzt. Eine Einschränkung z.B. der Anzahl der Buchstaben und Ziffern eines Identifikators kann mit den bisher beschriebenen Ausdrucksmitteln nicht ohne weiteres erfolgen. In der erweiterten Backus-Naur-Form wird deshalb die Potenz einer Zeichenreihe als Darstellungsmittel aufgenommen:
[...]exp n:m
Das Klammerpaar [...] umschließt die mindestens n-mal und maximal m-mal aneinander zu kettende syntaktische Konstruktion. Für
[...]exp n:n kann auch [...]exp n oder für [...]exp 0:oo (oo steht für unendlich) kann auch [...]exp* und für [...]exp 1:oo kann auch[...]exp+ sowie für [...]exp 0:1 kann auch [...] notiert werden. Oftmals werden in der erweiterten Backus-Naur-Form Alternativen durch die Auswahlklammerpaare {...} eingeschlossen untereinander notiert.
Die Backus-Naur-Regeln wurden in den 90er Jahren weiterentwickelt zur Augmented Backus Naur Form ( ABNF) und zur Extended Backus Naur Form (EBFN).