voltage standing wave ratio (VSWR)
Standingwaves occur when voltages, radio waves and sound waves are transmitted via cables or in free space. If signals are transmitted in cables that are not terminated with the cable impedance, then parts of the signal are reflected and transmitted in the cable in the opposite direction. The reflected signal part depends on the reflection factor.
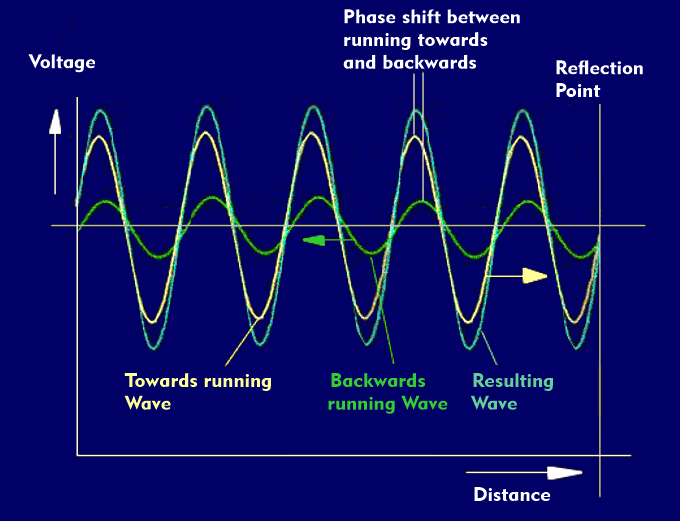
The wave traveling in the cable is then reflected at the end of the cable or at the connection between the cables and travels back in the cable. The returning wave interferes with the outgoing wave with which it is superimposed. Depending on the phase position of the outgoing and return waves, both waves can add up to a larger one or subtract to a smaller one. As a result, wave crests and troughs form on the cable at regular intervals. In the case of extreme mismatch, for example when the cable is open or shorted at the end, a total reflection occurs which can cause the two waves to add up to a double-sized wave or cancel each other out.
The standing wave ratio, Voltage Standing Wave Ratio (VSWR), is calculated from the ratio of maximum to minimum voltage. The maximum voltage is equal to the sum of the outgoing and return voltages, and the minimum voltage is determined from the difference of the two.
If, for example, the cable is optimally terminated with the correct characteristic impedance and the outgoing wave is assigned the voltage value 1, then the returning wave, due to the fact that no voltage is reflected, has the voltage value 0. The sum of both voltage values thus remains 1, the difference and the standing wave ratio likewise. The standing wave ratio of 1.00 thus corresponds to the optimum matching. For mismatches, the standing wave ratio increases until it goes to infinity for total mismatch.
The standing wave ratio can also be determined by the ratio of impedances. For example, if a 75-ohm cable is terminated with 100 ohms, then the standing wave ratio is 100/75 or 1.33. There is a direct relationship between the standing wave ratio and the reflection coefficient and return loss.
As a graphical representation for the standing wave ratio, the Smith chart is useful, which shows the complex impedances and admittances with their real and imaginary parts.

-mit-Spannungsmaxima-und-minima_en.png)
