co-ordinate system
In order to be able to determine positions in the plane or in space, one needs reference systems. A coordinate system is such a reference system. There are two- and multi-dimensional orthogonal coordinate systems with rectangular or geographic coordinates, with linear and logarithmically divided coordinates, but also circular ones like the polar coordinate system or the Smith chart.
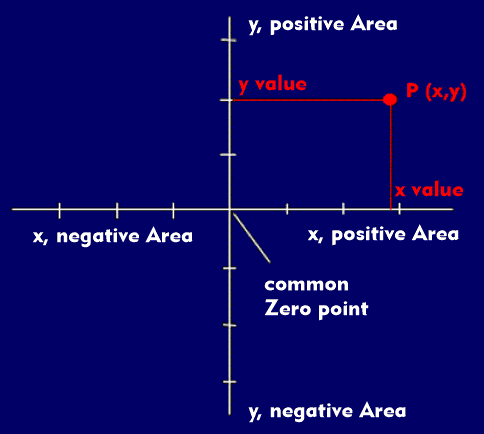
A two-dimensional Cartesian coordinate system uses two defined axes "X" and "Y" that are perpendicular to each other. The range of values, the dimension and the linearity of the values depends on the application. The axes run through the common reference point, the zero point (0/0), in both directions. The positive value range of the vertical axis lies above, that of the horizontal axis to the right of the zero point. The two axes can have a linear value range, but also a logarithmic, quadratic or exponential one. The value determination for a position results from the reference values of the abscissa (X) and the ordinate (Y). The Cartesian coordinate system can also be used for three-dimensional representations with an additional "Z" axis.
Three-dimensional Cartesian coordinate systems are built up accordingly, differ in the third coordinate, that is the Z-coordinate, which is arranged at right angles to the other two. With these three coordinates - XYZ - positions in space can be determined.
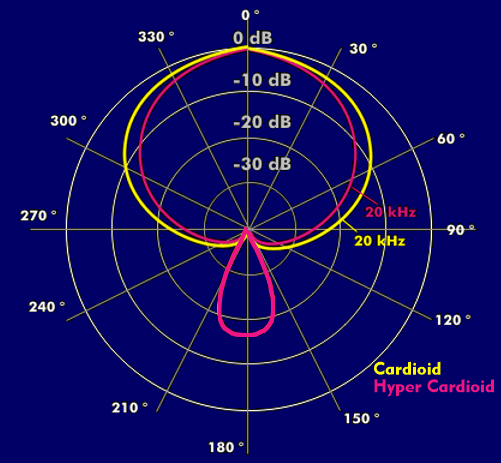
Polar coordinate systems are two-dimensional, circular coordinate systems. They are divided into uniform polar coordinates which have their origin in a fixed reference point, the pole. The polar coordinates can be divided in angular degrees. The pole is surrounded by several reference circles, whose radius corresponds to a second reference value - for example the level. By this representation form one has the possibility to enter level representations in dependence of the solid angle, as with the radiation characteristic ofantennas or the directional characteristic of microphones and loudspeakers.