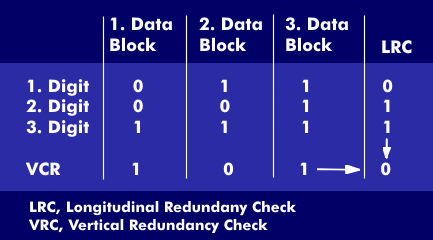
longitudinal redundancy check (LRC)
Longitudinal parity, Longitudinal Redundancy Check (LRC), is an error-protection method in which the cross sum of a data block is set to either even or odd parity by adding or not adding a parity bit.
The receiver of the message knows whether the parity is even or odd. It cannot tell if the message was transmitted intact, but it can detect errors if they are odd-numbered, i.e. 1, 3, 5, or 7...; an even-numbered number of errors cannot be detected by this method.
The longitudinal parity check is a very simple parity check forerror detection that can be implemented quickly. However, it is not very reliable, since it does not detect multiple errors or sequence swapping. It is therefore used for checking small blocks of data.