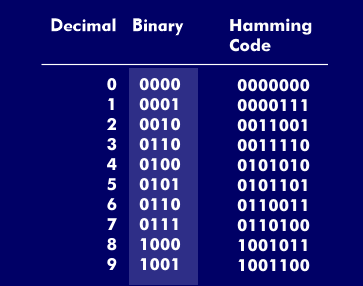
hamming code
Hamming coding is an error reduction method that is used wherever classical error correction cannot be used and data records containing errors can be requested again by the recipient. In these cases, high demands are placed on the error reduction procedure.
In Hamming code, the difference in bit structure from character to character is particularly large, so that the probability of complete correction of the character is maximized in the event of faulty data transmission. Unlike other error detection methods, the Hamming code uses multiple check bits and can detect multiple errors occurring simultaneously. In general, the number of check bits added to the redundancy of a data packet depends on the number of data bits transmitted. To reduce the probability of errors, the number of parity bits is chosen as large as possible in the Hamming code. These parity bits, which are added to the data bits on the transmit side, are chosen so that the bit sum results in even or odd parity.
The number of parity bits to be added depends on the number of data bits. For example, four check bits are needed for the secure transmission of eight data bits. For 16 data bits, there are 5 check bits, for 32 data bits, there are 6 check bits, and so on. The code words to be transmitted correspond to the sum of data bits and parity bits. Thus, 8 data bits and 4 check bits result in a codeword length of 12 bits. The difference between the codeword - 12 in the example - and the parity bits (4) is the Hamming distance. With such a Hamming code (12.8), faulty data packets containing up to four faulty bits can be detected, and two bit positions can be corrected. For this purpose, only some of the information locations in the codeword are completed to even parity.
With the Hamming code, where checkpoints are obtained from different parity checks, it is in principle possible to construct codes for error correction of more than one error.