root mean sqare (RMS)
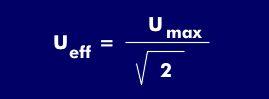
The RMS value is the root mean square (RMS) and represents the actual effective voltage, current or power values that occur. For example, the RMS value of an AC voltage is equivalent to that of a DC voltage, which produces the same amount of heat as the AC voltage. From the English designation Root Mean Square (RMS) it can be inferred that the effective value is the square root of the mean value of the square of the instantaneous amplitude.
For DC voltage, the RMS value corresponds to the DC voltage value. The RMS value of a pulse-shaped voltage is equal to half the peak voltage value of the pulse voltage if the duty cycle is 50%, i.e. the pulse duration and the pulse gap are equal. For sinusoidal voltages, the rms value is calculated from the ratio of the peak amplitude to the square root of two, which is 0.707 times the peak amplitude. The ratio between the rms value and the peak value is determined by the crest factor. For a sinusoidal signal, it has the value of root 2 = 1.414.
The rms value is an important characteristic value of the power supply. In Germany , the power grid has a nominal voltage of 230 V. This alternating voltage represents the effective value. The peak voltage is higher by a factor of 1.414, the peak-to-peak voltage corresponds to twice the peak voltage. In transmitting technology and transponders, too, the transmitting power is about the RMS value. In addition, the RMS value also plays an essential role in acoustics, as it indicates the value for the average load in an audio system that is closest to the perceived loudness.
In general, it should be noted that the RMS value is involved wherever the power of a simple or complex AC signal affects acoustic, electrical or optical communication. Thus in the determination of the distortion factor, distortions or the dynamic range.