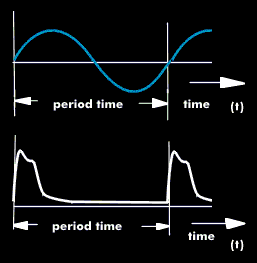
period (T)
The period is the time between two identical points on two successive oscillation trains of a periodic wave motion. The prerequisite for a period duration is a repeating oscillation form. This can be a sine or rectangular signal, a triangular signal, pulse signal or sawtooth signal or any other signal form.
Any reference point can be used to determine the period. For a sinusoidal signal or a square wave signal, it can be the zero crossing of the signal edge or the rising edge. However, the signal level must pass the zero potential in the same direction. However, it can also be any other point on the oscillation corresponding to a certain level and phase.
The period (T) is given in a unit of time in seconds, milliseconds or microseconds and is the quotient of the frequency (f): 'T = 1/f'. Example: A frequency of 1 kHz has a period of 1 ms.
Counters with high temporal resolution are used to determine the period duration, because this determines the measured accuracy. If a counter has a reference frequency of 10 MHz, then the maximum resolution is 100 ns. The period duration can therefore not be resolved higher than 100 ns.
There is a direct relationship between frequency, period duration and wavelength. As already mentioned, the period duration is the quotient of the frequency: The period duration is T = 1/f. On the other hand, the frequency can be determined from the quotient of the propagation velocity, it corresponds in free space to the speed of light (c), and the wavelength (`lambda`): `f = c/lambda`. From this results that the periodic time is the quotient of the wavelength and the speed of light: `T = lambda/c`.