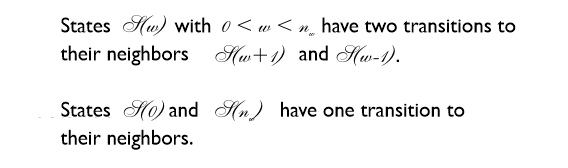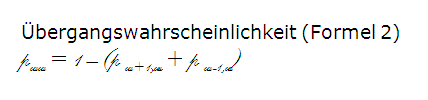Markov process
Markov processes, further notations: Markov or Markoff processes, represent a tool for modeling stochastic processes. The definition of Markov processes goes back to the Russian mathematician Andrej Markov (1856 - 1922). Markov processes are important for the description of processes in physics, natural sciences, economics and biology.
Markov processes characterize a stochastic process. A differentiation is made between continuous and discrete processes. If it is a discrete process, it is also called a Markov chain.
States and state transitions form the basic concept of Markov processes. Since this can be better imagined for discrete, at most countably many states and it also fits better to the discrete approach of waiting systems, the further representation is limited to Markov chains. During modeling, suitable states and state transitions must be defined. The consideration of chains also has the advantage that they can be represented graphically as a state graph.
A stochastic process is called a Markov process if these conditions are met (formula 1).
The Markov property now states that a next state always depends only on the just current one and not on the previous history, especially not on the initial state. The current state thus contains everything that needs to be known about the past.
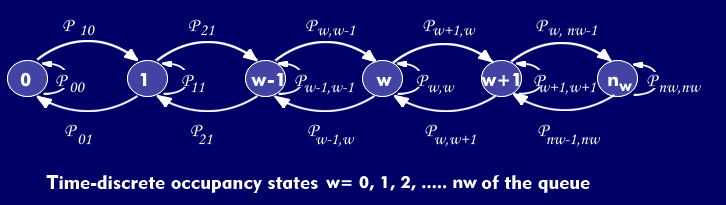
The Markov chain is used to describe the stochastic occupancy behavior of the queue. The circles model the possible occupancy states of the queue and the directed marked edges of the graph (arrows) model the state transitions, where the transition from state "i" to state "j" occurs with the transition probability p(ij) i .
The Markov chain shown is characterized by the fact that each state has transitions only to its immediate neighbors, but not to more distant states. Since the number of states is limited, all states have exactly two transitions to their neighbors. Two states each have only one transition to their neighbors.
In the discrete-time case shown, each occupancy state also has one more transition to itself with the transition probability (formula 2).
In general, the future random behavior of a Markov chain at any time "t" depends only on the even active state, but not on the past random behavior that activated the state. This applies directly to the occupancy behavior of the memory of a queueing system as well.