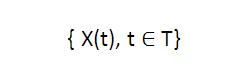Stochastische Prozesse sind Familien (auch: Mengen) von Zufallsvariablen X(t), die durch einen Parameter t gekennzeichnet sind. Dabei durchläuft t einen geeigneten Parameterraum R und wird in den meisten Anwendungen als Zeit gedeutet. T ist dann eine Folge von Zeitpunkten oder ein Zeitintervall. Gegenüber der "klassischen" Stochastik, bei der der zeitlich statische Fall im Vordergrund steht, werden in der Theorie der stochastischen Prozesse die zeitlich dynamischen Aspekte im Verhalten von Zufallsvariablen untersucht.
Da es sich bei stochastischen Prozessen letztendlich um verallgemeinerte Zufallsexperimente handelt, spricht man in diesem Zusammenhang auch von zufälligen Funktionen oder zufälligen Prozessen.
Zur Vereinfachung der Darstellung und im Hinblick auf die übergroße Anzahl der Anwendungen wird im Folgenden der Parameter t bei der Darstellung der theoretischen Grundlagen als Zeit interpretiert. Somit ist X(t) die interessierende Zufallsgröße zum Zeitpunkt t, während T den gesamten Betrachtungszeitraum umfasst. Z bezeichnet die Menge aller Zustände (auch Realisierungen genannt), die die X(t) annehmen können.
Definition des stochastischen Prozesses
Unter einem stochastischen Prozess mit dem Parameterraum T und dem Zustandsraum Z versteht man die Menge der Zufallsgrößen.
Ist die Parametermenge endlich oder abzählbar unendlich, spricht man von einem stochastischen Prozess mit diskreter Zeit. Derartige Prozesse lassen sich in Folge von Zufallsgrößen aufschreiben: {X(1), X(2) ... }. Umgekehrt lässt sich jede Folge von Zufallsgrößen als stochastischer Prozess mit diskreter Zeit interpretieren. Ist T ein Intervall, dann spricht man von einem stochastischen Prozess mit stetiger Zeit.
Der stochastische Prozess (siehe Abbildung) heißt diskret, wenn sein Zustandsraum Z eine endiche oder eine abzählbar unendliche Menge ist. Dagegen liegt ein stetiger stochastischer Prozess vor, wenn Z ein Intervall ist.
Der Zeitbezug von stochastischen Prozessen
Es gibt diskrete stochastische Prozesse mit diskreter Zeit, diskrete stochastische Prozesse mit stetiger Zeit, stetige stochastische Prozesse mit diskreter Zeit sowie stetige stochastische Prozesse mit stetiger Zeit.
Zur Erfassung möglicher Abhängigkeiten zufälliger Größen von deterministischen Parametern geht man vom Begriff der Zufallsgröße zu dem des stochastischen Prozesses (auch: Zufallsprozess) über. So sind beispielsweise die Bewegung der Moleküle eines Gases, der Wasserstand in einem Stausee, Winderregungen, Erdbebenerregungen, die Anzahl der Kunden in einer Warteschlange, die Anzahl von Telefonanrufen, Niederschlagsmenge u.v.a., in Abhängigkeit von der Zeit betrachtet, stochastische Prozesse. Praktisch bedeutsame Typen stochastischer Prozesse sind Markov-Prozesse, Gausssche Prozesse, stationäre Prozesse, Poissonsche Prozesse, Wienersche Prozesse, Diffusionsprozesse, Prozesse mit unabhängigen Zuwächsen, Martingale, Verzweigungsprozesse sowie Punktprozesse.
Die Klassifikation stochastischer Prozesse kann nach den verschiedensten Merkmalen erfolgen, wie z.B. der Verteilungsfunktionen, der Kovarianzfunktionen, der Parametermenge und der Realisierungen.