Das Smith-Diagramm, Smith-Chart, ist eine grafische Darstellung mit der relativ komplizierte mathematische Zusammenhänge durch ein geometrisches Konstrukt ersetzt werden. Bei dieser Darstellung werden komplexe Zahlen übersichtlich dargestellt, wodurch man impedanzmäßige Änderungen auf Hochfrequenzkabeln oder anderen HF-Komponenten darstellen kann. Es zeigt dem Benutzer wie sich die Impedanz oder Admittanz aufgrund des Reflexionsfaktors oder des Stehwellenverhältnisses ( VSWR) bei verschiedenen Frequenzen verhält.
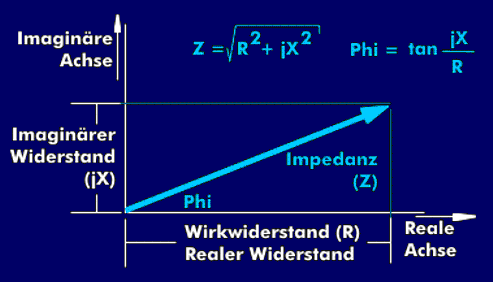
Die klassische Darstellung der Impedanzen erfolgt im kartesischen Koordinatensystem, wobei die realen und imaginären Anteile in beiden Achsen des Koordinatensystems dargestellt werden. Ihre Anteile sind bestimmt durch den Betrag (Z) und den Winkel (Phi). Ändern sich der reale und der imaginäre Widerstand, dann ändern sich die beiden Größen "Z" und Phi. Eine andere Darstellungsform ist die polare, die im Smith-Diagramm benutzt wird, allerdings als normierte, dimensionslose Impedanz.
Aufbau der Smith-Chart
Bei dem Smith-Chart handelt es sich um ein kreisförmiges Koordinatensystem für die Darstellung komplexer Impedanzen von frequenzabhängigen Zweipolen, Vierpolen oder HF-Schaltungen. Dargestellt werden Streuparameter, Stehwellenverhältnisse und Reflexionskoeffizienten auf einem kreisförmigen Koordinatensystem, das die Impedanz- oder Admittanzwerte repräsentiert. In der Horizontalen der Smith-Chart werden die realen Werte aufgetragen.
Bei der Darstellung über das Stehwellenverhältnis können diese Werte zwischen "0" und unendlich liegen. In der Vertikalen liegen die imaginären Werte +jx und -jx, ebenfalls zwischen "0" und unendlich. Die Horizontalachse ist logarithmisch eingeteilt, jeder Wert zwischen "0" und unendlich wird durch einen Kreis dargestellt. Der äußerste Kreis entspricht dem Wert "0", die folgenden Kreise haben Durchmesser, die dem reziproken Logarithmus entsprechen. Der Kreis der durch den Mittelpunkt des 0-Kreises geht, entspricht dem Wert "1". Die vertikalen Kreise für die imaginären Werte schneiden die Kreise für die realen Werte im Winkel von 90°.
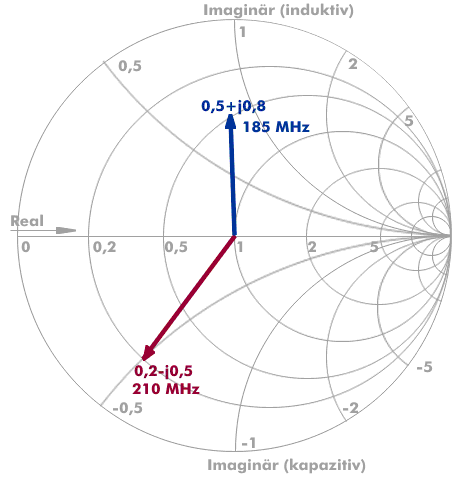
Die obere Hälfte der Smith-Chart stellt den induktiven Blindwiderstand dar, die untere den kapazitiven. In diesen Kreisdiagrammen wird die normierte Impedanz als komplexe dimensionslose Zahl dargestellt. Ist kein Blindwiderstand vorhanden und ändert sich die reale Impedanz mit der Frequenz, dann entsteht ein Vektor auf der Horizontalen.
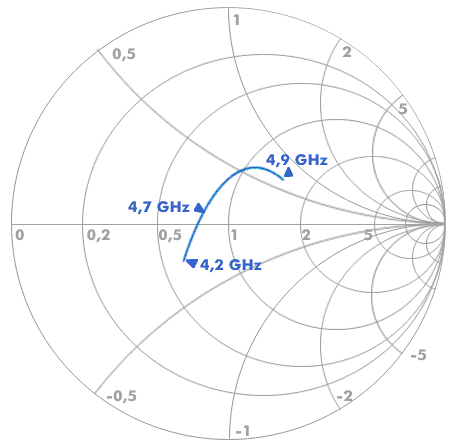
Bei einer anderen Frequenz ergibt sich eine andere Impedanz und somit ein weiterer Vektor, der auch einen imaginären Anteil haben kann. Die Größe der Vektoren ist ein Maß für das Stehwellenverhältnis. Die Endpunkte der Vektoren werden miteinander verbunden und es entsteht eine Kurvenform, die die Vektorendpunkte bei den einzelnen Frequenzen darstellt. Da es in dem Smith-Diagramm keine frequenzmäßigen Bezug gibt, müssen die einzelnen Frequenzen in der Chart markiert werden.
Darstellung mit dem Smith-Chart
Mit dem Smith-Diagramm wird das Stehwellenverhalten von Vierpolen dargestellt. Das können HF-Stecker, Hochfrequenzkabel oder Antennen sein.
Der Name der Smith-Chart ist auf dessen Entwickler Philip Smith von den Bell Labs zurückzuführen, der die Smith-Chart in den 30er Jahren entwickelte.