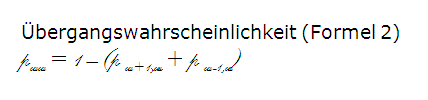Markov-Prozesse, weitere Schreibweisen: Markow- oder Markoff-Prozesse, stellen ein Hilfsmittel zur Modellierung stochastischer Prozesse dar. Die Definition der Markov-Prozesse geht zurück auf den russischen Mathematiker Andrej Markov (1856 - 1922). Die Markov-Prozesse sind bedeutsam für die Beschreibung von Vorgängen in der Physik, den Natur- und Wirtschaftswissenschaften oder auch in der Biologie.
Markov-Prozesse kennzeichnen einen stochastischen Prozess. Dabei wird differenziert zwischen kontinuierlichen und diskreten Prozessen. Handelt es sich dabei um einen diskreten Prozess, so wird dieser auch als Markov-Kette bezeichnet.
Zustände und Zustandsübergänge bilden das Grundkonzept von Markov-Prozessen. Da sich dies für diskrete, maximal zählbar viele Zustände besser vorstellen lässt und es auch besser zur diskreten Betrachtungsweise von Wartesystemen passt, beschränkt sich die weitere Darstelllung auf Markov-Ketten. Bei der Modellierung müssen geeignete Zustände und Zustandsübergänge definiert werden. Die Betrachtung von Ketten hat zudem den Vorteil, dass man diese als Zustandsgraph anschaulich darstellen kann.
Ein stochastischer Prozess heißt Markov-Prozess, falls diese Voraussetzungen erfüllt sind (Formel 1).
Die Markov-Eigenschaft besagt nun, dass ein nächster Zustand immer nur von dem gerade aktuellen abhängt und nicht von der Vorgeschichte, insbesondere auch nicht vom Startzustand. Im aktuellen Zustand ist somit alles enthalten, was über die Vergangenheit bekannt sein muss.
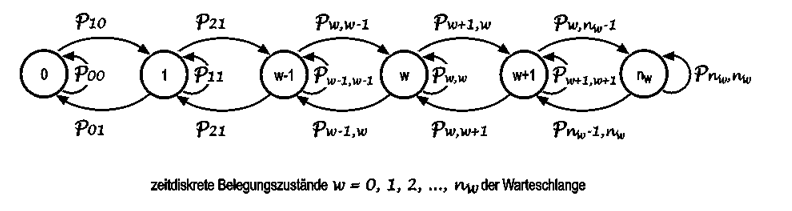
Zur Beschreibung des stochastischen Belegungsverhaltens der Warteschlange dient die Markov-Kette. Die Kreise modellieren die möglichen Belegungszustände der Warteschlange und die gerichteten markierten Kanten des Graphen (Pfeile) die Zustandsübergänge, wobei der Übergang von Zustand "i" in den Zustand "j" mit der Übergangswahrscheinlichkeit p(ij) i erfolgt.
Die gezeigte Markov-Kette ist dadurch gekennzeichnet, dass jeder Zustand nur Übergänge zu seinen unmittelbaren Nachbarn hat, nicht aber zu weiter entfernten Zuständen. Da die Anzahl der Zustände begrenzt ist, haben alle Zustände genau zwei Übergänge zu ihren Nachbarn. Zwei Zustände haben jeweils nur einen Übergang zur ihren Nachbarn.
Im dargestellten zeitdiskreten Fall hat außerdem jeder Belegungszustand noch einen Übergang zu sich selbst mit der Übergangswahrscheinlichkeit (Formel 2).
Im Allgemeinen ist das zukünftige Zufallsverhalten einer Markov-Kette zu jedem Zeitpunkt "t" nur von dem geraden aktiven Zustand abhängig, nicht jedoch von dem vergangenen Zufallsverhalten, das den Zustand aktiviert hat. Diese gilt unmittelbar auch für das Belegungsverhalten des Speichers eines Wartesystems.